Wave–particle duality. . . .

In 1905, Albert Einstein provided an explanation of the photoelectric effect, a hitherto troubling experiment that the wave theory of light seemed incapable of explaining. He did so by postulating the existence of photons, quanta of light energy with particulate qualities.

In the photoelectric effect, it was observed that shining a light on certain metals would lead to an electric current in a circuit. Presumably, the light was knocking electrons out of the metal, causing current to flow. However, using the case of potassium as an example, it was also observed that while a dim blue light was enough to cause a current, even the strongest, brightest red light available with the technology of the time caused no current at all. According to the classical theory of light and matter, the strength or amplitude of a light wave was in proportion to its brightness: a bright light should have been easily strong enough to create a large current. Yet, oddly, this was not so.

Einstein explained this enigma by postulating that the electrons can receive energy from electromagnetic field only in discrete portions (quanta that were called photons): an amount of energy E that was related to the frequency f of the light by

${\displaystyle E=hf\,}$

where h is Planck's constant (6.626 × 10⁻³⁴ J seconds). Only photons of a high enough frequency (above a certain threshold value) could knock an electron free. For example, photons of blue light had sufficient energy to free an electron from the metal, but photons of red light did not. One photon of light above the threshold frequency could release only one electron; the higher the frequency of a photon, the higher the kinetic energy of the emitted electron, but no amount of light (using technology available at the time) below the threshold frequency could release an electron. To "violate" this law would require extremely high-intensity lasers which had not yet been invented. Intensity-dependent phenomena have now been studied in detail with such lasers.

Einstein was awarded the Nobel Prize in Physics in 1921 for his discovery of the law of the photoelectric effect.

De Broglie's wavelength

Main article: Matter wave

Propagation of de Broglie waves in 1d—real part of the complex amplitude is blue, imaginary part is green. The probability (shown as the colour opacity) of finding the particle at a given point x is spread out like a waveform; there is no definite position of the particle. As the amplitude increases above zero thecurvature decreases, so the amplitude decreases again, and vice versa—the result is an alternating amplitude: a wave. Top: Plane wave. Bottom: Wave packet.

In 1924, Louis-Victor de Broglie formulated the de Broglie hypothesis, claiming that all matter, not just light, has a wave-like nature; he related wavelength (denoted as λ), and momentum (denoted as p):

${\displaystyle \lambda ={\frac {h}{p}}}$

This is a generalization of Einstein's equation above, since the momentum of a photon is given by p = ${\displaystyle {\tfrac {E}{c}}}$ and the wavelength (in a vacuum) by λ = ${\displaystyle {\tfrac {c}{f}}}$, where c is the speed of light in vacuum.

De Broglie's formula was confirmed three years later for electrons (which differ from photons in having a rest mass) with the observation of electron diffraction in two independent experiments. At the University of Aberdeen, George Paget Thomsonpassed a beam of electrons through a thin metal film and observed the predicted interference patterns. At Bell Labs, Clinton Joseph Davisson and Lester Halbert Germer guided their beam through a crystalline grid.

De Broglie was awarded the Nobel Prize for Physics in 1929 for his hypothesis. Thomson and Davisson shared the Nobel Prize for Physics in 1937 for their experimental work.

Heisenberg's uncertainty principle

Main article: Heisenberg uncertainty principle

In his work on formulating quantum mechanics, Werner Heisenberg postulated his uncertainty principle, which states:

${\displaystyle \Delta x\Delta p\geq {\frac {\hbar }{2}}}$

where

${\displaystyle \Delta }$ here indicates standard deviation, a measure of spread or uncertainty;

x and p are a particle's position and linear momentum respectively.

${\displaystyle \hbar }$ is the reduced Planck's constant (Planck's constant divided by 2${\displaystyle \pi }$).

Heisenberg originally explained this as a consequence of the process of measuring: Measuring position accurately would disturb momentum and vice versa, offering an example (the "gamma-ray microscope") that depended crucially on the de Broglie hypothesis. The thought is now, however, that this only partly explains the phenomenon, but that the uncertainty also exists in the particle itself, even before the measurement is made.

In fact, the modern explanation of the uncertainty principle, extending the Copenhagen interpretation first put forward by Bohrand Heisenberg, depends even more centrally on the wave nature of a particle: Just as it is nonsensical to discuss the precise location of a wave on a string, particles do not have perfectly precise positions; likewise, just as it is nonsensical to discuss the wavelength of a "pulse" wave traveling down a string, particles do not have perfectly precise momenta (which corresponds to the inverse of wavelength). Moreover, when position is relatively well defined, the wave is pulse-like and has a very ill-defined wavelength (and thus momentum). And conversely, when momentum (and thus wavelength) is relatively well defined, the wave looks long and sinusoidal, and therefore it has a very ill-defined position.

de Broglie–Bohr theory

Couder experiments,"materializing" the pilot wave model.

De Broglie himself had proposed a pilot wave construct to explain the observed wave-particle duality. In this view, each particle has a well-defined position and momentum, but is guided by a wave function derived from Schrödinger's equation. The pilot wave theory was initially rejected because it generated non-local effects when applied to systems involving more than one particle. Non-locality, however, soon became established as an integral feature of quantum theory (see EPR paradox), and David Bohm extended de Broglie's model to explicitly include it.

In the resulting representation, also called the de Broglie–Bohm theory or Bohmian mechanics, the wave-particle duality vanishes, and explains the wave behaviour as a scattering with wave appearance, because the particle's motion is subject to a guiding equation orquantum potential. "This idea seems to me so natural and simple, to resolve the wave-particle dilemma in such a clear and ordinary way, that it is a great mystery to me that it was so generally ignored", J.S.Bell.

The best illustration of the pilot-wave model was given by Couder's 2010 "walking droplets" experiments, demonstrating the pilot-wave behaviour in a macroscopic mechanical analog..

Wave behavior of large objects

Since the demonstrations of wave-like properties in photons and electrons, similar experiments have been conducted with neutrons and protons. Among the most famous experiments are those of Estermann and Otto Stern in 1929 Authors of similar recent experiments with atoms and molecules, described below, claim that these larger particles also act like waves. A wave is basically a group of particles which moves in a particular form of motion, i.e. to and fro. If we break that flow by an object it will convert into radiants.

A dramatic series of experiments emphasizing the action of gravity in relation to wave–particle duality was conducted in the 1970s using the neutron interferometer.Neutrons, one of the components of the atomic nucleus, provide much of the mass of a nucleus and thus of ordinary matter. In the neutron interferometer, they act as quantum-mechanical waves directly subject to the force of gravity. While the results were not surprising since gravity was known to act on everything, including light (see tests of general relativity and the Pound–Rebka falling photon experiment), the self-interference of the quantum mechanical wave of a massive fermion in a gravitational field had never been experimentally confirmed before.

In 1999, the diffraction of C₆₀ fullerenes by researchers from the University of Vienna was reported. Fullerenes are comparatively large and massive objects, having an atomic mass of about 720 u. The de Broglie wavelength of the incident beam was about 2.5 pm, whereas the diameter of the molecule is about 1 nm, about 400 times larger. In 2012, these far-field diffraction experiments could be extended to phthalocyanine molecules and their heavier derivatives, which are composed of 58 and 114 atoms respectively. In these experiments the build-up of such interference patterns could be recorded in real time and with single molecule sensitivity.

In 2003, the Vienna group also demonstrated the wave nature of tetraphenylporphyrin—a flat biodye with an extension of about 2 nm and a mass of 614 u. For this demonstration they employed a near-field Talbot Lau interferometer. In the same interferometer they also found interference fringes for C₆₀F_48., a fluorinated buckyball with a mass of about 1600 u, composed of 108 atoms. Large molecules are already so complex that they give experimental access to some aspects of the quantum-classical interface, i.e., to certain decoherence mechanisms. In 2011, the interference of molecules as heavy as 6910 u could be demonstrated in a Kapitza–Dirac–Talbot–Lau interferometer. In 2013, the interference of molecules beyond 10,000 u has been demonstrated.

Whether objects heavier than the Planck mass (about the weight of a large bacterium) have a de Broglie wavelength is theoretically unclear and experimentally unreachable; above the Planck mass a particle's Compton wavelength would be smaller than the Planck length and its own Schwarzschild radius, a scale at which current theories of physics may break down or need to be replaced by more general ones.

Recently Couder, Fort, et al. showed that we can use macroscopic oil droplets on a vibrating surface as a model of wave–particle duality—localized droplet creates periodical waves around and interaction with them leads to quantum-like phenomena: interference in double-slit experiment, unpredictable tunneling (depending in complicated way on practically hidden state of field), orbit quantization (that particle has to 'find a resonance' with field perturbations it creates—after one orbit, its internal phase has to return to the initial state) and Zeeman effect.

Treatment in modern quantum mechanics

Wave–particle duality is deeply embedded into the foundations of quantum mechanics. the formalism of the theory, all the information about a particle is encoded in its wave function, a complex-valued function roughly analogous to the amplitude of a wave at each point in space. This function evolves according to a differential equation (generically called the Schrödinger equation). For particles with mass this equation has solutions that follow the form of the wave equation. Propagation of such waves leads to wave-like phenomena such as interference and diffraction. Particles without mass, like photons, have no solutions of the Schrödinger equation so have another wave.

The particle-like behavior is most evident due to phenomena associated with measurement in quantum mechanics. Upon measuring the location of the particle, the particle will be forced into a more localized state as given by the uncertainty principle. When viewed through this formalism, the measurement of the wave function will randomly "collapse", or rather "decohere", to a sharply peaked function at some location. For particles with mass the likelihood of detecting the particle at any particular location is equal to the squared amplitude of the wave function there. The measurement will return a well-defined position, (subject to uncertainty), a property traditionally associated with particles. It is important to note that a measurement is only a particular type of interaction where some data is recorded and the measured quantity is forced into a particular eigenstate. The act of measurement is therefore not fundamentally different from any other interaction.

Following the development of quantum field theory the ambiguity disappeared. The field permits solutions that follow the wave equation, which are referred to as the wave functions. The term particle is used to label the irreducible representations of the Lorentz group that are permitted by the field. An interaction as in a Feynman diagram is accepted as a calculationally convenient approximation where the outgoing legs are known to be simplifications of the propagation and the internal lines are for some order in an expansion of the field interaction. Since the field is non-local and quantized, the phenomena which previously were thought of as paradoxes are explained. Within the limits of the wave-particle duality the quantum field theory gives the same results.

Visualization

There are two ways to visualize the wave-particle behaviour: by the "standard model", described below; and by the Broglie–Bohm model, where no duality is perceived.

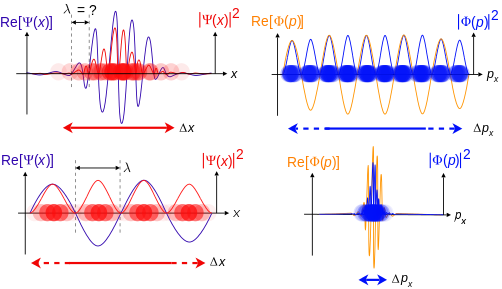
Below is an illustration of wave–particle duality as it relates to De Broglie's hypothesis and Heisenberg's uncertainty principle (above), in terms of the position and momentum space wavefunctions for one spinless particle with mass in one dimension. These wavefunctions are Fourier transforms of each other.

The more localized the position-space wavefunction, the more likely the particle is to be found with the position coordinates in that region, and correspondingly the momentum-space wavefunction is less localized so the possible momentum components the particle could have are more widespread.

Conversely the more localized the momentum-space wavefunction, the more likely the particle is to be found with those values of momentum components in that region, and correspondingly the less localized the position-space wavefunction, so the position coordinates the particle could occupy are more widespread.

Position x and momentum p wavefunctions corresponding to quantum particles. The colour opacity (%) of the particles corresponds to the probability density of finding the particle with position x or momentum component p.
Top: If wavelength λ is unknown, so are momentum p, wave-vector k and energy E (de Broglie relations). As the particle is more localized in position space, Δx is smaller than for Δp_x.
Bottom: If λ is known, so are p, k, and E. As the particle is more localized in momentum space, Δp is smaller than for Δx.

Alternative views

Wave–particle duality is an ongoing conundrum in modern physics. Most physicists accept wave-particle duality as the best explanation for a broad range of observed phenomena; however, it is not without controversy. Alternative views are also presented here. These views are not generally accepted by mainstream physics, but serve as a basis for valuable discussion within the community.

Both-particle-and-wave view

The pilot wave model, originally developed by Louis de Broglie and further developed by David Bohm into the hidden variable theory proposes that there is no duality, but rather a system exhibits both particle properties and wave properties simultaneously, and particles are guided, in a deterministic fashion, by the pilot wave (or its "quantum potential") which will direct them to areas of constructive interference in preference to areas of destructive interference. This idea is held by a significant minority within the physics community.

At least one physicist considers the "wave-duality" as not being an incomprehensible mystery. L.E. Ballentine, Quantum Mechanics, A Modern Development, p. 4, explains:

When first discovered, particle diffraction was a source of great puzzlement. Are "particles" really "waves?" In the early experiments, the diffraction patterns were detected holistically by means of a photographic plate, which could not detect individual particles. As a result, the notion grew that particle and wave properties were mutually incompatible, or complementary, in the sense that different measurement apparatuses would be required to observe them. That idea, however, was only an unfortunate generalization from a technological limitation. Today it is possible to detect the arrival of individual electrons, and to see the diffraction pattern emerge as a statistical pattern made up of many small spots (Tonomura et al., 1989). Evidently, quantum particles are indeed particles, but whose behaviour is very different from classical physics would have us to expect.

The Afshar experiment (2007) may suggest that it is possible to simultaneously observe both wave and particle properties of photons. This claim is, however, disputed by other scientists.

Wave-only view

At least one scientist proposes that the duality can be replaced by a "wave-only" view. In his book Collective Electrodynamics: Quantum Foundations of Electromagnetism (2000),Carver Mead purports to analyze the behavior of electrons and photons purely in terms of electron wave functions, and attributes the apparent particle-like behavior to quantization effects and eigenstates. According to reviewer David Haddon:

Mead has cut the Gordian knot of quantum complementarity. He claims that atoms, with their neutrons, protons, and electrons, are not particles at all but pure waves of matter. Mead cites as the gross evidence of the exclusively wave nature of both light and matter the discovery between 1933 and 1996 of ten examples of pure wave phenomena, including the ubiquitous laser of CD players, the self-propagating electrical currents of superconductors, and the Bose–Einstein condensate of atoms.

Albert Einstein, who, in his search for a Unified Field Theory, did not accept wave-particle duality, wrote,

This double nature of radiation (and of material corpuscles)...has been interpreted by quantum-mechanics in an ingenious and amazingly successful fashion. This interpretation...appears to me as only a temporary way out...

The many-worlds interpretation (MWI) is sometimes presented as a waves-only theory, including by its originator, Hugh Everett who referred to MWI as "the wave interpretation".

The Three Wave Hypothesis of R. Horodecki relates the particle to wave.The hypothesis implies that a massive particle is an intrinsically spatially as well as temporally extended wave phenomenon by a nonlinear law.

Particle-only view

Still in the days of the old quantum theory, a pre-quantum-mechanical version of wave–particle duality was pioneered by William Duane,and developed by others includingAlfred Landé Duane explained diffraction of x-rays by a crystal in terms solely of their particle aspect. The deflection of the trajectory of each diffracted photon was explained as due to quantized momentum transfer from the spatially regular structure of the diffracting crystal.

Neither-wave-nor-particle view

It has been argued that there are never exact particles or waves, but only some compromise or intermediate between them. For this reason, in 1928 Arthur Eddington coined the name "wavicle" to describe the objects although it is not regularly used today. One consideration is that zero-dimensional mathematical points cannot be observed. Another is that the formal representation of such points, the Dirac delta function is unphysical, because it cannot be normalized. Parallel arguments apply to pure wave states. Roger Penrose states:

"Such 'position states' are idealized wavefunctions in the opposite sense from the momentum states. Whereas the momentum states are infinitely spread out, the position states are infinitely concentrated. Neither is normalizable [...]."

Relational approach to wave–particle duality

Relational quantum mechanics is developed which regards the detection event as establishing a relationship between the quantized field and the detector. The inherent ambiguity associated with applying Heisenberg's uncertainty principle and thus wave–particle duality is subsequently avoided.

Applications

Although it is difficult to draw a line separating wave–particle duality from the rest of quantum mechanics, it is nevertheless possible to list some applications of this basic idea.

• Wave–particle duality is exploited in electron microscopy, where the small wavelengths associated with the electron can be used to view objects much smaller than what is visible using visible light.
• Similarly, neutron diffraction uses neutrons with a wavelength of about 0.1 nm, the typical spacing of atoms in a solid, to determine the structure of solids.
• Photos are now able to show this dual nature, which may lead to new ways of examining and recording this behaviour.